在当今数据驱动的时代，时间序列分析已成为众多领域研究的热点，向量自回归模型（Vector Autoregression Model，简称VAR模型）作为一种重要的统计模型，广泛应用于经济、金融、生物医学等领域的时间序列数据分析，本文将介绍向量自回归模型的基本原理、应用及其优势。

向量自回归模型的基本原理

向量自回归模型是一种动态模型，用于分析多个时间序列变量之间的相互影响和因果关系，VAR模型将每个时间序列变量视为一个向量，通过构建一个包含多个变量的线性回归方程来预测未来值，VAR模型的基本形式可以表示为：

yt = A1yt-1 + A2yt-2 + ... + Apyt-p + εt

yt是k维向量，包含k个时间序列变量；yt-i表示滞后i期的向量；Ai是系数矩阵；εt是随机扰动项，p表示模型的滞后阶数，即用于预测的历史数据点的数量。

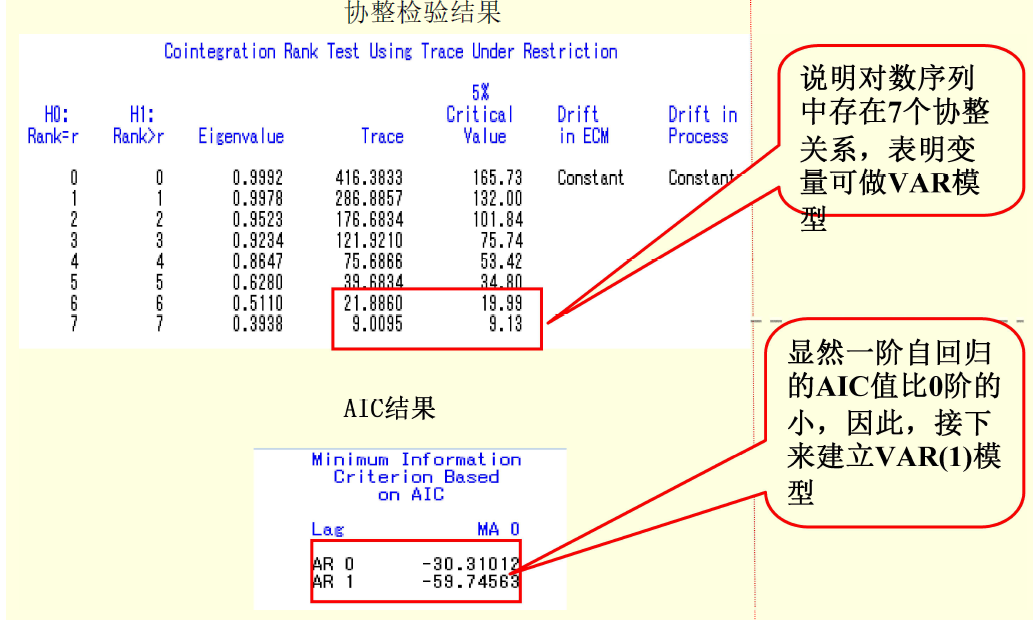
VAR模型的关键在于确定合适的滞后阶数p和系数矩阵Ai，通过估计这些参数，我们可以了解时间序列变量之间的动态关系，并预测未来趋势。

向量自回归模型的应用

1、宏观经济预测

VAR模型广泛应用于宏观经济预测，如GDP增长率、通货膨胀率、失业率等经济指标的预测，通过构建包含多个经济指标的VAR模型，可以分析这些指标之间的相互影响，提高预测的准确性。

2、金融风险管理

在金融领域，VAR模型被广泛应用于风险管理，通过构建包含股票价格、汇率、利率等金融指标的VAR模型，可以分析金融市场的时间序列数据，识别潜在的风险因素，为投资决策提供有力支持。

3、生物医学数据分析

在生物医学领域，VAR模型被应用于分析基因表达数据、疾病发病率等时间序列数据，通过构建包含多个生物指标的VAR模型，可以揭示生物过程之间的相互作用，为疾病诊断和治疗提供新的思路。

向量自回归模型的优势

1、揭示时间序列变量之间的动态关系

VAR模型能够揭示多个时间序列变量之间的相互影响和因果关系，有助于我们深入了解数据的内在规律。

2、预测未来趋势

通过估计VAR模型的参数，我们可以预测时间序列数据的未来趋势，为决策提供支持。

3、易于处理季节性数据和非平稳数据

VAR模型能够处理季节性数据和非平稳数据，使得在时间序列分析中具有更广泛的应用范围。

向量自回归模型作为一种重要的统计模型，广泛应用于经济、金融、生物医学等领域的时间序列数据分析，通过构建包含多个变量的线性回归方程，VAR模型能够揭示时间序列变量之间的相互影响和因果关系，预测未来趋势，在实际应用中，我们需要根据数据的特性选择合适的滞后阶数和系数矩阵，以确保模型的准确性和可靠性，随着数据量的不断增加和计算能力的提升，VAR模型将在更多领域得到广泛应用，为决策提供更加准确和全面的支持。

展望与不足

尽管向量自回归模型在时间序列数据分析中表现出强大的优势，但仍存在一些局限性，VAR模型的滞后阶数选择和参数估计需要一定的经验和技巧，VAR模型假设随机扰动项是无关的，但在实际数据中可能存在噪声和异常值的影响，VAR模型无法处理非线性关系和非平稳过程的问题，未来研究可以进一步探讨如何改进VAR模型的参数估计方法，提高其鲁棒性和适应性，以应对更复杂的时间序列数据分析问题，结合其他机器学习算法和统计方法，可以进一步提高VAR模型的预测性能和应用范围，随着数据科学和人工智能的不断发展，向量自回归模型将在时间序列数据分析中发挥更加重要的作用。